Lesson 2/Learning Event 1
Mathematical Method for Determination of n. A table of logarithms or a calculator with a logarithm
function is needed to determine n using the mathematical method. A table of logarithms is in Appendix
A on page 105. The mathematical determination of the decay exponent is accomplished by solving the
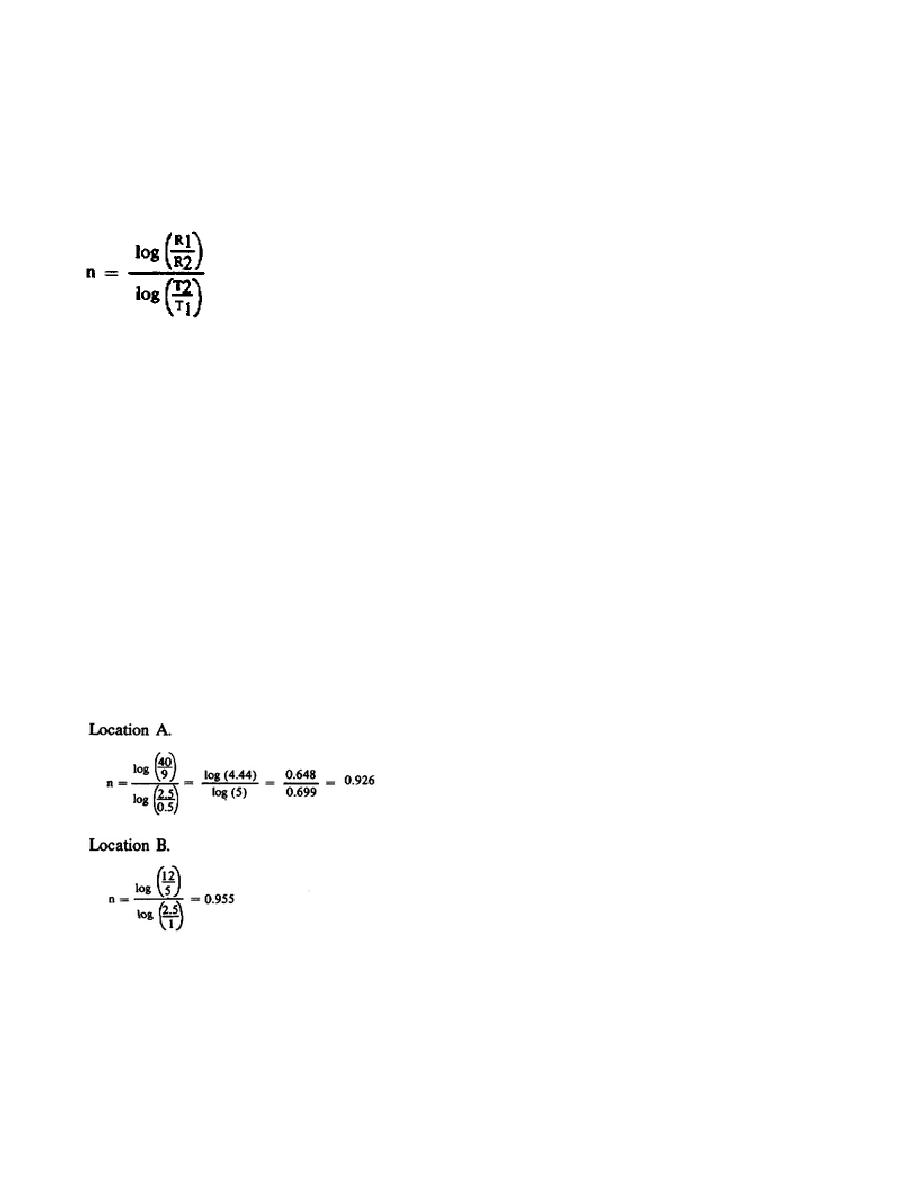
Kaufman equation for n. The Kaufman equation is:
In the equation, the time and dose rate of the earlier reading is represented by T1 and R1 and the time and
dose rate of the later reading is represented by T2 and R2.
A logarithm table to base 10 in Appendix A can be used to determine the log of the quotient from the
parenthetical fraction (R1/R2) and (T2/T1). Logarithms are divided into two parts: the characteristic,
which is the whole number part and the mantissa, which is the decimal part of the logarithm. The
characteristic is determined by the value of the quotient. If this number is 0 - 10, the characteristic of the
log is 0. If the number is 10 - 100, the characteristic of the log is 1, and so on up the scale. The
mantissa is determined by reading down the N column of the log table to the value of the first two
numbers of the quotient and across the table to the third number. As an example, to determine the log of
4.44, we must first determine the characteristic. Since 4 is less than 10, the characteristic of the
logarithm is 0. To determine the mantissa, enter the logarithm table in the N column and read down to
44, then across the table to the column under the 4. Here you read the mantissa as 6474; therefore, the
log of 4.44 is written as 0.647 when rounded off to the nearest thousandth.
Monitoring data is applied to this formula, using beginning and end point dose rates as shown below.
The data are from the situation discussed in the graphical determination of n.
40




 Previous Page
Previous Page
